容斥原理
S表示面积,下面公式可求出不相交的面积
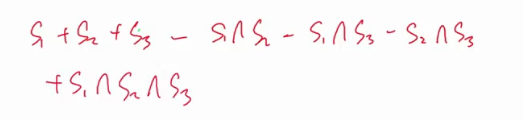

2个圆的公式是这样
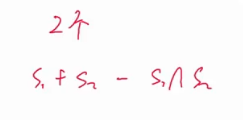
4个圆的面积是
总面积-所有俩俩相交的面积+所有三三相交的面积-四四相交的面积,公式里加和减互相出现。
从n个集合里面挑一个一直到从n个集合里面挑n个
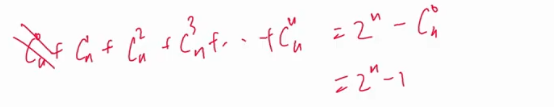
1-10中,能被2,3整除的数是下面打勾的

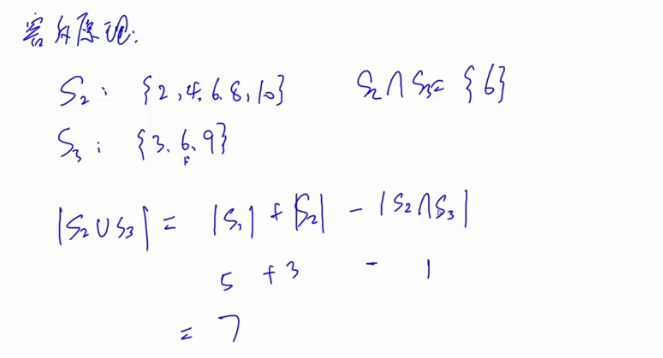
p能整除n的个数,是n/p

p不能整除n的个数是n/p取整
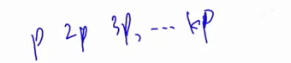
这里共有2的n次方-1项

从n个集合当中选若干个集合,所有的选法都在上述公式中,每种选法的符号跟我们所选取的奇偶数有关,我们用位来表示,如果某位为0,则代表没有选,为1,则代表被选。
其他博主写的比较好的题解

#include
#include
using namespace std;
typedef long long LL;
const int N = 20;
int n, m;
int p[N];
int main()
{
cin >> n >> m;
for (int i = 0; i > p[i];//把5个质数读进来
int res = 0;
//从1开始枚举到2的m次方,即枚举了2的m次方-1个数
//这里把2的m次方写成了位运算的格式
for (int i = 1; i > j & 1)
{
cnt++;
if ((LL)t * p[j] > n)//如果t*p[j]>n就不用算了
{
t = -1;
break;
}
t *= p[j];
}
if (t != -1)//此时说明这几个的乘积小于等于n
{
if (cnt % 2) res += n / t;//奇数个集合是加,偶数个集合是减
else res -= n / t;
}
}
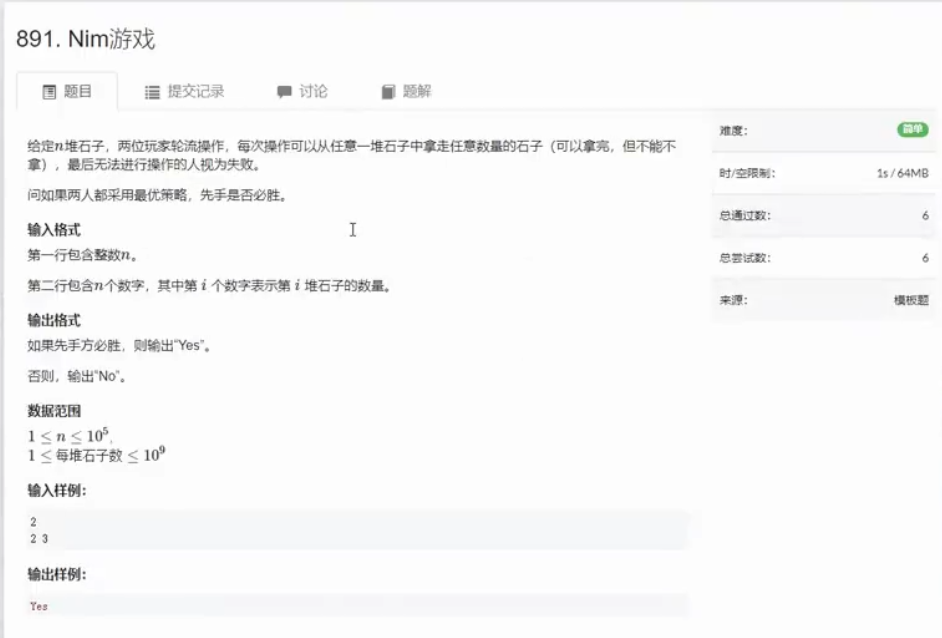
cout 博弈论
先手必败状态:对方必应。
先手必胜状态:自己拿完之后,对手再拿,对手必输。
这里是异或

如果异或值不是0,我们可以从某一堆中拿走一些石子,让剩下的值异或变成0,即先拿的可以决定后拿的结果。
若最开始的异或值是0,则先手的结果一定是0,后手的结果就不是0,即先手拿到的永远是0,后手拿到的永远不是0.
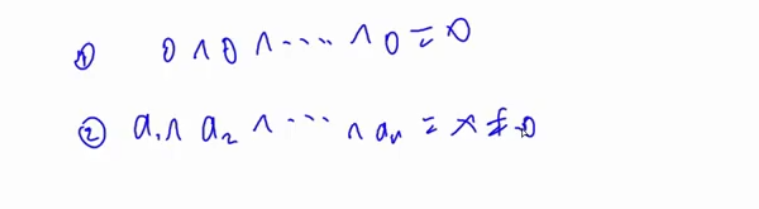
Nim游戏
int main()
{
int n;
int res = 0;
scanf("%d", &n);
while (n--)
{
int x;
scanf("%d", &x);
res ^= x;
}
if (res) puts("Yes");
else puts("No");
return 0;
}集合——Nim游戏

集合1,2,3中找出的是0
SG函数
任何非0的状态都能到0,任何0状态到不了0状态,
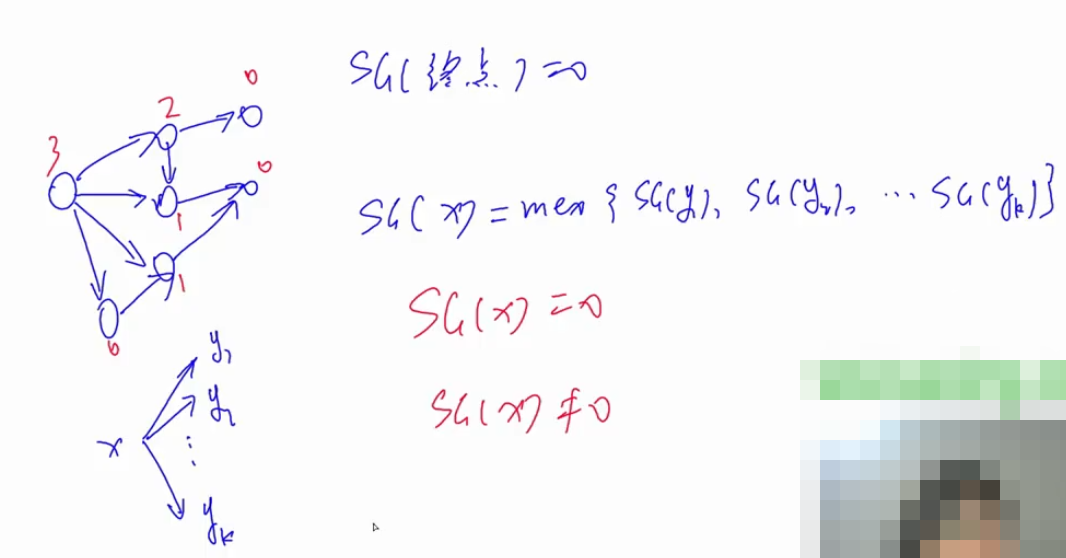
如果当前所有局面异或起来不是0,我们可以把它变成0,如果是0,我们都可以让他不是0
下面这个例子限定了每次取石子的个数
即有3个堆,分别有2,4,7个石子,每次取得时候只能取2个或5个,如果取 不到就失败

假如只有一堆,而且这一堆有10个,每次只能取2或5,每次取完后得结果可以这样表示
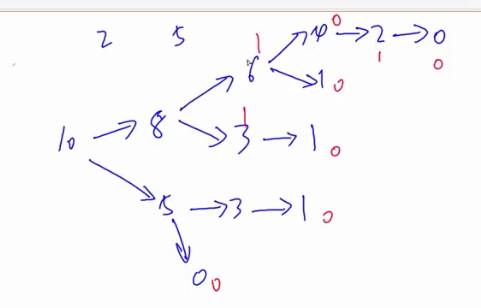
参考题解
【ACWing】893. 集合-Nim游戏_记录算法题解的博客-CSDN博客
(1条消息) [AcWing] 893. 集合-Nim游戏(C++实现)博弈论SG函数模板题_Cloudeeeee的博客-CSDN博客_博弈论c++
#include
#include
const int N = 110, M = 10010;
int n, m;
int s[N], f[M];// s存能取哪些个数的石子,f表示sg得值。
int sg(int x)
{
if(f[x]!= -1) return f[x];//记忆化搜索,每个状态只计算一次
unordered_set S;//用哈希表存储可以到达得局面
for (int i = 0; i = sum)//如果当前数的个数大于等于sum,也就是能取,如要取俩个石子,当前总共有8个,8>=2;
S.insert(sg(x - sum)); // 将新的状态加进来
}
for (int i = 0;; i++)// 找出集合当中不存在的最小值并返回
if (!S.count(i))//如果当前这个数不存在,直接返回
return f[x] = i;
}
int main()
{
cin >> m;
for (int i = 0; i > s[i];
cin >> n;
memset(f, -1, sizeof f);
int res = 0;
for (int i = 0; i > x;
res ^= sg(x);
}
if (res) puts("Yes");
else puts("No");
return 0;
}
服务器托管,北京服务器托管,服务器租用 http://www.fwqtg.net

